Fizika

Az első részben egy olyan megközelítésével találkoztunk a speciális relativitás elméletnek, aminek révén igen egyszerűen sikerült belátni a világegyetem modelljeként szolgáló téridő, vagy másképpen mondva elektromágneses mező  különböző pontjainak függetlenségét. Bár minden különböző pontban ugyanazok a természettörvények érvényesek, de az idő minden különböző pontban másképpen telik, és a különböző pontok között kizárólag a téridő, vagy elektromágneses mező teremt kapcsolatot, méghozzá kizárólag fénysebességű rezgései által. Ez a kapcsolat pedig olyan, hogy bizonyos körülmények, például a relatív mozgások hatással vannak a különböző időtartamok egybevethetőségére.

Nem árt tudni, hogy nem csak a relatív mozgások befolyásolják az időtartamok egybevethetőségét, hanem a nagy tömegek (bolygók, csillagok, galaxisok, galaxis halmazok) is elgörbítik a téridőt (elektromágneses mezőt), így a nagy tömegek is befolyásolják az időtartamok egybevethetőségét. Ez utóbbi jelenségek tárgyalása azonban az általános relativitás elmélet keretébe tartozik, és bonyolult matematikája miatt nem képezi tárgyát jelenlegi vizsgálatainknak, csupán a teljesség kedvéért említettem meg. Kisebb tömegek esetében ez a téridő görbület nem jelentős, így vagy elhanyagolható, vagy a Newton-féle gravitációs vonzástörvényekkel helyettesíthető.

A Doppler-eltolódás jelensége lehetőséget adott, hogy a téridő relativitását érzékeltessük, és kiszámíthassuk. Ez azért lehetséges, mert az eltolódás szimmetriáját leíró képletben (A nyugalomban f frekvenciájú fényforráshoz egy adott sebességgel közeledve f*s Doppler-eltolódást szenvedő fény ugyanezen sebességű távolodáskor f/s Doppler-eltolódást szenved) a frekvencia tetszőleges volt, vagyis egy tetszőleges mérték konverzióját, transzformációját írta le, és közvetetten, de pontosan meghatározott módon a sebesség és az idődilatáció összefüggését is leírja. Persze ez a transzformáció is csak akkor alkalmazható, ha a kibocsájtó és észlelő elmozdulása egy vonalban, az összekötő egyenesük vonalában történik. Más térbeli irányokba történő elmozdulásokra csak annyi állítható, hogy az összekötő egyenesre való vetület sebessége (vagyis a távolság változása) határozza meg a Doppler-eltolódás mértékét, de ebből nem lehet következtetni sem a kibocsájtó és észlelő tényleges sebességeire, sem az ebből következő idődilatációra, távolságkontrakcióra. Tehát ilyen esetben más módszereket kell találnunk. Ezért is írtam korábban, hogy a hagyományos tanulmányi kurzusokat nem lehet megspórolni a cikkeim olvasása útján, talán csupán barátságosabbá, könnyebben megérthetővé válnak ezek a kurzusok a cikkeim által. Azt is fontos megjegyezni, hogy az itt tapasztalati tényként bevezetett Doppler-eltolódás az elméleti alapok fejezetben felsorolt többi összefüggésből levezethető, tehát nem számít sem axiómának, sem posztulátumnak. A speciális relativitás elmélet megalapozásának szokásos kurzusai ennek menetét pontosan tartalmazzák, én itt erre nem térek ki.

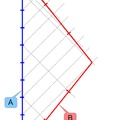
De hogy ne maradjunk számításra való okoskodás nélkül ebben a leckében sem, egy speciális esetre mégis meghatározzuk az idődilatációt. Egy olyan esetre, amelyben a mozgó objektum távolsága nem változik a megfigyelőtől, vagy legalábbis ez a távolság változás elhanyagolható. Ehhez az előző ikerparadoxonos példából indulunk ki, és veszünk egy harmadik megfigyelőt, Csabát (C), aki Antallal azonos inercia rendszerben nyugszik, és az ikreket nagyon messziről, egy elég távoli jövőből (>100év) figyeli meg olyan helyről, hogy Béla űrhajója az utazása negyedén, és háromnegyedén éppen merőlegesen halad hozzá képest, tehát Csaba és Béla távolsága nem, vagy alig változik, így Csaba nem érzékel Doppler-eltolódást. Antal azonban kap egy újabb fényjelző készüléket, amely Csaba irányába világít, és csak akkor villan fel, amikor Bélától érkezik egy fényjel. Tehát ez csak egy fényjel közvetítő (szokásos nevén: tükör). Emiatt Csaba ugyanazokat a felvillanásokat észleli Antall felől, amit Antall érzékel Béla felől. Béla utazása Csaba saját órája szerint is 10 évig tart, és Antallal megegyezően ugyanúgy Béla 6 évre való felvillanásait veszi. De amíg Antall felől két különböző szakaszban 1/3 és 3 Hz frekvenciával jönnek a jelek, addig Béla felől egyenletesen kell jönniük a jeleknek, hiszen erről nincs Doppler-eltolódás. Ez csak akkor lehetséges, ha Béla felől végig 5/3 Hz frekvenciával jönnek a jelek, vagyis a 0,6-es idődilatáció szerint. Béla oldalirányú mozgása Csaba által is látható, és a látószög változásából Csaba is kiszámíthatja Béla 4/5 c sebességét. Ezen eredmények tükrében mindjárt sokkal több értelmet kap az idődilatáció fogalma, ami az előző cikkben magyarázat nélkül maradt.