Talán a fizika oktatása szempontjából sem érdektelen, ahogyan az einsteini speciális relativitás-elméletet a saját számítási példámon keresztül ismertetem, amelyben a könnyebb megértést segítve csak a négy matematikai alapművelet használatára szorítkozom, így tárgyalásom akár nélkülözheti az első kivételével a newton törvények ismeretét, és akár az általános iskola alsó tagozatán is megérthető. Ez a példa persze nem helyettesíti mindazt az elméleti tudást, amit erről a témáról mások leírtak, de megmutatja, hogy ugyanazt a feladatot néha sokkal könnyebben, sokkal kevesebb erőfeszítéssel meg lehet oldani, ha a célnak legmegfelelőbb helyes összefüggéseket használjuk fel.

Elméleti alapok

A matematika, és a fizika alapvető fogalma a koordináta rendszer, amely fogalmat a középkor első nagy gondolkodója, René Descartes vezette be. A három dimenziós térben bármely pont helyzete megadható a térben három egymásra merőleges tengellyel megadott koordináta rendszer segítségével úgy, hogy a pont koordináta tengelyekre való vetületén leolvassuk a tengelyen levő koordináta értékeket. A koordináta tengelyeket általában x,y,z betűkkel jelöljük. Mivel a fizikai jelenségeknél többnyire a mozgásokat is vizsgáljuk, így az időpont rögzítése is fontos a pontok koordinátáin kívül, amelyhez a t betűvel jelölt időtengelyt használjuk, így a mozgások esetében négy koordinátával (x,y,z,t) számolunk. Egy térben mozgó pont esetén az időtengely minden t koordinátaértékéhez tartozik egyetlen térbeli koordináta (x,y,z), így egy mozgó pont egy folytonos vonalként jelenik meg a négydimenziós koordináta rendszerben, amit ezen szoros kapcsolat miatt téridőnek is neveznek, és ez a vonal a múltból halad a jövő felé. A koordináta rendszer csak akkor használható jól, ha az egy szilárdan rögzített viszonyítási alap, tehát önmaga nem végez semmilyen mozgást. Hiszen a koordináta rendszer saját mozgása hozzáadódik a vizsgált pontok mozgásához, és meghamisítja a pontok görbéit. Sajnos azonban ilyen fix viszonyítási alap nem létezik a világban, ezt már az ókorban Arkhimédész is emlegette híres mondásában (Adjatok egy fix pontot, és kimozdítom helyéből a világot). Így bizonyos engedményeket kell tenni a koordináta rendszer kijelölésénél. Általában könnyen észlelünk saját egyensúlyérzékünkkel bizonyos mozgás fajtákat, mint például a gyorsulást (lassulást), a fordulást, és a forgást. A legtöbb esetben észleljük az állandó sebességű egyenes vonalú haladást is, de bizonyos esetekben ezt nem vesszük észre. Galileo Galilei megmutatta, hogy ha nincs külső viszonyítási alapunk, akkor az állandó sebességű egyenes vonalú mozgás nem mutatható ki, míg más mozgások esetén erő hat ránk.

Mint ahogyan a Newton-féle mozgástörvények esetében is, a speciális relativitás elméletnek is alapvető fogalma az inercia rendszer. Ez egy olyan nem forgó térbeli (x,y,z) és időbeli (t) koordináta rendszert jelent, amelynek egy kiválasztott koordinátáját egy olyan szabadon mozgó ponthoz rögzítünk, amelyre nem hat erő. Mint tudni való, Newton első törvénye értelmében egy test, amelyre nem hat erő, vagy nyugalomban van, vagy egyenes vonalban egyenletes sebességgel mozog. A Földön ezt először nehéz elképzelni, mivel a földi tárgyak mozgását lelassítja a légellenállás, a súrlódás, és a mozgó testek pályáját pedig elgörbíti a Föld gravitációs tere. Tehát ilyen erőmentes lebegés csak az űrben az égitestektől távol található, de ott is korlátozottan, hiszen nagyon sok égitest van. A különböző inercia rendszerek egymáshoz képest csak állandó sebességű egyenes vonalú mozgást végezhetnek, és egyenértékűek a természettörvények leírása szempontjából (Galilei-féle relativitás elv).

A vákuumbeli fénysebesség bármely inerciarendszerből nézve ugyanaz az adott c állandó (c = 1 fényév/év = kb. 300 000 km/s), és a fény vákuumban minden irányban azonos módon egyenes vonalban terjed. Összehasonlításként a Föld kerülete az egyenlítőnél 40 000 km, tehát a fény ennek 7 és félszeresét teszi meg egy másodperc alatt. Egy adott inerciarendszerhez rögzített fényforrás fényének adott állandó frekvenciája egy másik inerciarendszerből nézve Doppler-eltolódást szenvedhet. Ezt a jelenséget már 50 évvel a speciális relativitás elmélet megalkotása előtt felfedezték. Távolodáskor a megfigyelt frekvencia csökken, közeledéskor a megfigyelt frekvencia növekszik. Tehát ha elébe megyünk egy ismétlődő, véges sebességgel terjedő jelnek, akkor sűrűbben ismétlődőnek tapasztaljuk, ha távolodunk tőle, akkor ritkábban ismétlődőnek. A változásra a vákuumbeli fénysebesség esetére egy nagyon egyszerűen számszerűsíthető szabály is vonatkozik. A nyugalomban f frekvenciájú fényforráshoz egy adott v sebességgel közeledve f*s Doppler-eltolódást szenvedő fény (ahol s egy dimenzió nélküli viszonyszám) ugyanezen sebességű (-v) távolodáskor f/s Doppler-eltolódást szenved. (Bár itt most tapasztalati törvényként vezettük be ezt az összefüggést, valójában levezethető a többi alapelvből is, de az egyszerűbb tárgyalás kedvéért ettől most eltekintünk.) Ennek a fontos törvénynek fizikai értelmezéseként állíthatjuk, hogy a tér nem csupán üres vákuum. A teret elektromágneses mező tölti ki, vagy mondhatnánk úgy is, hogy a tér maga az elektromágneses mező, amelynek rezgései (a fény is ilyen rezgés) minden inerciarendszerből nézve fénysebességgel, és egyenes vonalban terjednek (vákuumban). Ugyanis a Doppler-eltolódás mindig valamilyen közegre vonatkozik. Az elektromágneses mező ezen tulajdonsága lehetővé teszi, hogy az inerciarendszereket egyértelműen azonosítani tudjuk, és minden ettől való eltérést pontosan érzékeljünk a mező rezgéseinek Doppler-effektus miatti megváltozásán. Így a mozgásállapot változásoknál mindig egyértelmű, melyik test a mozgásállapota változik, a mozgásállapot megváltozására nem érvényes a relativitás elve. Tehát ha nem érzékelünk az elektromágneses mező rezgéseiben semmilyen irányban Doppler-eltolódás változást, akkor inercia rendszerben vagyunk. Ha az elektromágneses mező rezgéseiben adott irányban változást tapasztalunk, akkor ebben az irányban változik a mozgásunk. Az univerzumot betöltő elektromágneses mező állandó rezgésben van, mivel azt a csillagok fényei, és az univerzum átlagosan 2,7 Kelvin hőmérsékleti sugárzása folyamatos rezgésben tartja, így a létező univerzum mindig telített elektromágneses rezgésekkel, így nem fordulhat elő olyan eset, hogy a Doppler-eltolódást ne érzékelhetnénk a rezgések hiánya miatt. A térben nincsenek semmilyen más (például azonos idejű) kapcsolatok a tér különböző pontjaiban levő objektumok között, mint az elektromágneses mező (és vele a téridő) fénysebességű rezgései, amelyek egyben a múlt, és jövő közötti kapcsolatokat is jelentik. Hogy a gyorsulás nem relatív, az persze már az inerciarendszer definíciójából is egyértelmű, feltéve, hogy legalább három tehetetlen pont létezését feltételezzük, hiszen ekkor már minden pont helyzete legalább két másik ponthoz viszonyítható. A világegyetemben viszont szinte megszámlálhatatlan viszonyítási ponttal számolhatunk (pontos számuk nem ismerhető meg), de például egy űrhajó is igen sok pontból áll ahhoz, hogy megállapítható legyen a reá ható gyorsító erő.

A négydimenziós (három térszerű, és egy időszerű koordináta) téridő különböző pontjai egyenértékűek, tehát mindenhol ugyanazok a természet-törvények érvényesek. Vagyis a természet-törvények sem időben, sem térben nem változnak. Így tehát a születésünkkor nullázott, és állandóan velünk levő pontos óra híven mutatja a korunkat, függetlenül attól, hogy milyen utakat járunk be közben térben, és időben, és ezt a kormeghatározást bármely más tárgy esetében is alkalmazhatjuk. (Itt feltételezzük azt is, hogy az óra működését nem befolyásolja a nem inerciális mozgás.) Az inercia rendszerekben használatos, és az azokhoz rögzített időmértékektől eltérően ezt az időt sajátidőnek nevezzük, tehát a sajátidő mindig egy adott objektumhoz rögzített időmérték, ami egyébként a négydimenziós téridőben az objektum életvonalának, vagy annak vizsgált intervallumának a hossza. Emlékeztetőül a (3D) térben való nyugvás, vagy mozgás, a (4D) téridőben egyenes, vagy görbe életvonalként jelenik meg.

Az alábbi példából majd látni fogjuk, a speciális relativitás elmélet ezen elvei alapján, és ezekből következően az olyan mennyiségeknek, mint a térbeli távolságoknak, vagy az eltelt időtartamoknak csak adott inerciarendszerhez kötötten vannak adott meghatározott értékeik. Egy másik inerciarendszerben ezek az értékek különbözhetnek, és az értékek különbözősége egyértelműen meghatározható az inerciarendszerek egymáshoz képesti sebességéből. Tudomásul kell venni, hogy a téridő különböző pontjai függetlenek egymástól, és ezen egyenértékű pontok az összeköttetés speciális jellege folytán nem mutatkoznak egyenértékűnek bizonyos összehasonlításokban. Így a különböző, egymáshoz képest mozgó objektumok életvonalainak az objektumok találkozásai közötti szakaszain általában különböző sajátidő hosszúságok adódnak.

Lássuk ezt az úgynevezett ikerparadoxon példáján

A paradoxon elnevezés arra utal, hogy ha a mozgásállapot-változást is relatívnak vehetnénk, akkor szimmetrikus lenne a példában Antal (A), és Béla (B) helyzete, így az ikrek korkülönbségét nem lehetne mivel magyarázni. De mivel a mozgásállapot-változásra a relativitás nem áll, így természetesen szó nincs valódi paradoxonról, csak egy furcsaságról a hétköznapi szemléletünkben. A példában az átlagsebességre vonatkozó jól ismert $v=s/t, \; s=v*t, \; t=s/v$ összefüggéseket használom (ahol $v$: átlagsebesség, $s$: út, $t$: idő). Mivel a példában csak egyetlen koordináta tengely menti mozgások fordulnak elő, ezért az x,y,z koordináták használata helyett elégséges az s (út) használata.

Antal és Béla ikertestvérek. Antal végig egy helyben marad egy inerciarendszerben. Béla űrhajóval elutazik hatalmas sebességgel. Mindegyikük rendelkezik egy-egy pontos másodpercenként felvillanó (f=1 Herz) órával, és mindegyikük láthatja a másikuk órájának villanásait Béla teljes utazása alatt. Béla űrhajója olyan erős hajtóművel van ellátva, hogy a gyorsulás időtartalmainak elemzésétől eltekinthetünk, úgy vehetjük, hogy ez az utazás időtartalmához képest elhanyagolható idő alatt megtörténik, mondhatni pillanatszerűen. Béla saját órája szerint 3 évig (=t_B) távolodik egyenes vonalban állandó sebességgel (azaz súlytalanul lebegve), majd visszafordulva ugyancsak 3 évig közeledik Antalhoz képest ugyanekkora, de ellentétes irányú állandó sebességgel. A fordulás ugyancsak olyan hatalmas gyorsulással történik, hogy annak időtartama elhanyagolható, mondhatni pillanatszerű. Az űrhajó utazási sebessége olyan óriási (később meghatározzuk), hogy Béla csak harmad annyi gyakorisággal (d_r=3) 1/3 herzesnek (=d₁=f/d_r) látja a tőle egyre távolabb kerülő Antal óráját a Doppler-eltolódás miatt, vagyis 3 másodpercenként lát egy felvillanást. Ebből Béla könnyen megállapíthatja, hogy 3 éves távolodása alatt Antal mindössze 1 évre (=t_B*d₁) való órajelei érkeznek el hozzá. Amikor Béla ellenkező irányt vesz űrhajójával, egészen mást fog tapasztalni. Antal órajele ettől fogva 3 herzes (=d₂=f*d_r) lesz a Doppler-eltolódás miatt, vagyis másodpercenként három felvillanást lát, így a 3 éves hazaútja során Antal 9 évi órajelét (=t_B*d₂) foghatja.

Ebből következőleg Béla megállapítja, hogy a saját idejében mért 6 éves( =2*t_B) utazása alatt Antal 10 évnyi órajelét vette (=t_B*d₁ + t_B*d₂=2*t_A) , ami csak úgy lehetséges, ha közben Antal 10 évet öregedett, míg Béla csak 6 évet. Ezzel a speciális relativitás elmélet egyik különös következményét, a lokális időtartamok (sajátidők) relativitását ismertük meg. Az idődilatáció mértéke 0,6 (=t_B/t_A).

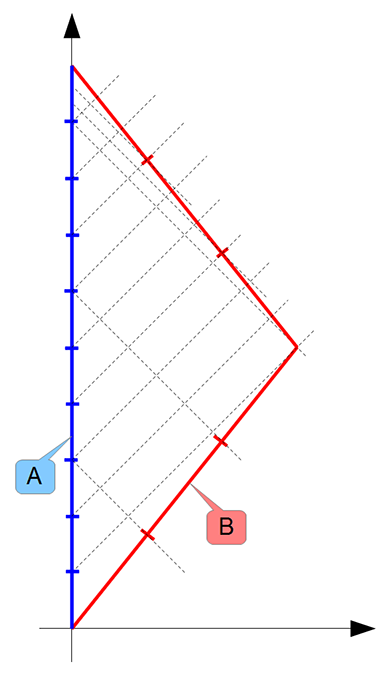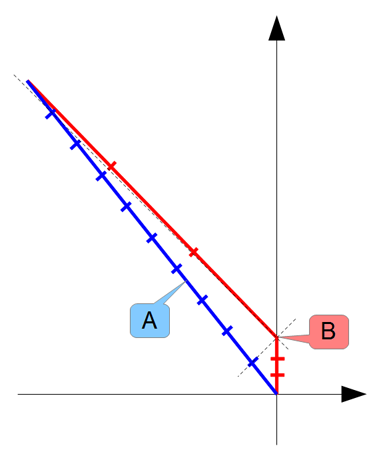
(A képeken az un. Minkowski-diagramon láthatjuk az ikrek életvonalait A nyugalmi inerciarendszerében. A függőleges tengelyen az időt, a vízszintes tengelyen az elmozdulást ábrázoljuk, tehát ez a téridőnek egy olyan metszete, amelyben az időtengely is ábrázolva van, és mivel a mozgás csak egyetlen térbeli kiterjedést érint, így a teljes egydimenziós útvonalat ábrázolhatjuk ebben a metszetben. A 45 fokos szaggatott vonalak egységnyi (fényév/év) sebességű fényjeleket ábrázolnak. Az útvonalakon levő osztások A és B sajátideje évei múlásának felelnek meg. Mivel A inerciarendszerében vagyunk, így a nyugvó A ideje egyben a rendszeridő is.)

Antal ugyancsak 1/3 herzesnek (=d₁=f/d_r) látja a távozó Béla órajelét, és könnyen kiszámíthatjuk, hogy így Béla 3 évig sugárzott órajeleit 9 éven (=t_B*d₂) keresztül kell fogadnia Antalnak. Ezután még 1 évig (=t_B*d₁) veszi a közeledő Béla 3 évig sugárzott Antal számára 3 herzesnek (=d₂=f*d_r) mutatkozó jelét. Vagyis találkozásukkor Antal megállapítja, hogy 4 évvel (=2*t_A-2*t_B) idősebb lett Bélánál, tehát mind Antal, mind Béla egybehangzóan ugyanezt állapítja meg az egymástól fogadott órajelek mennyisége alapján. Ha emellett az órájuk az eltelt időt is mutatnák, akkor azok is nyilván 4 évnyi eltérést mutatnának az induláskori azonos állással szemben.

Mivel Béla az utazása felezőpontján fordult meg, így utazása időben szimmetrikus, ezért a fordulás Antal inerciarendszerében ábrázolva is félidőben történt, de eltérő időtartam, vagyis Antal szerint 5 év után (=t_A). Mivel a fordulást Antal csak az indulást követő 9-ik év után észleli, így a fényjelnek 4 évig (=t_cA=t_B*d₂-t_A) tartott, hogy az utazás legtávolabbi pontjától (s_A=c*t_cA=4 fényév) Antalhoz érjen. Így Antal inercia rendszerében Béla 4 fényévnyit utazott 5 év alatt, így sebessége igen tetemes, (v_AB=s_A/t_A=) 4 fényév/5 év = 0,8c.

Béla is természetesen ugyanezt a sebességet mérheti (v_AB=v_BA), lévén az inerciarendszerek egyenértékűek, de számára a távolodás csak 3 évig (=t_B) tartott, így az általa megtett távolságot is csak 2,4 fényévnyinek (=s_B=v_BA*t_B=0,8 fényév/év * 3 év) számolja. Pontosabban számára relatíve Antal távolodott ekkora sebességgel 2,4 fényévnyire, amíg ő az űrhajóban nyugodott Tehát a speciális relativitás elméletben a távolságok is relatívak, az inerciarendszer megválasztásától függnek. A távolság-kontrakció mértéke is 0,6 (=s_B/s_A).

Még határozzuk meg, hogy Bélának milyen sebesség-változásra van szüksége, amikor félúton megfordul, mivel itt nem alkalmazható a Newton törvények szerinti sebesség összegzési módszer. Ennek kiszámítását végig abban az inerciarendszerben végezzük, amelyhez képest Béla nyugalomban volt az útja első felében. Ez alatt Béla 3 évig vette Antal 1 év alatt kisugárzott jeleit, miközben Antal 0,8 c sebességgel távolodott ezen inerciarendszerben a most meghatározandó s_BA pontig, és Antal órajelei is fénysebességgel száguldottak vissza Bélához az s_BA pontból 3 év – s_BA/0,8c idő alatt. Vagyis
s_BA= c * (3év – s_BA/0,8c) = 3 fényév – s_BA/0,8,
s_BA + s_BA/0,8 = 9/4 s_BA = 3 fényév,
s_BA = 4/3 fényév.

Mivel az s_BA pont eléréséig Antal 1 évnyit öregedett, így a teljes útja alatt, amely számára 10 évig tartott, 10*s_BA = 40/3 fényévnyi távolságra jut el. Antal sebessége 0,8 c, így ilyen távolságra való eljutásának időtartalma 40/3 fényév/0,8c = 50/3 év.

Bélának ugyanekkorra (50/3 év), és ugyanide (40/3 fényév) kell eljutnia az újra találkozásukhoz, de 3 évvel később indulva, így Béla utazására csak 50/3 év-3 év = 41/3 év marad. A szükséges sebesség így (40/3 fényév) / (41/3 év) = 40/41 c. Vagyis Bélának ezzel a sebességgel kell megfordulnia a távolodási útszakaszához képest, hogy Antal inerciarendszeréből nézve a sebessége éppen ellentétes irányú, de azonos nagyságú legyen.

Ebből látszik az is tehát, hogy egy adott inerciarendszerben mozgó két test ezen inercia rendszerbeli sebességeiből viszonylag bonyolult összefüggés szerint lehet csak meghatározni a két test egymáshoz képesti relatív sebességét. Ezt relativisztikus sebesség-összeadásnak nevezik. Ezt az általános összefüggést nem határozzuk itt meg, azt azonban általánosságban is ki lehet jelenteni, hogy két test relatív sebessége sohasem lehet nagyobb a fénysebességnél, sőt még fénysebesség is csak akkor lehet, ha legalább az egyik test tömeg nélküli, mondjuk fénysugár. Ez esetben viszont ez a tömeg nélküli test minden más testhez képest (akár tömeg nélkülihez is) fénysebességű.

A modellből kihagytuk azokat a külső tényezőzőket (például állócsillagokat), amelyek a mozgásállapot változásokat egyértelművé teszik, mivel a számításokban ezek nem játszanak szerepet, de feltételezzük, hogy Béla és Antal is pontosan tudja mi történt, amikor az 1/3 herzes jelek 3 herzesre váltottak, hiszen előre megtervezték az utazást. Utólag amúgy is egyértelmű, hogy A és B helyzete nem szimmetrikus, hiszen ez a váltás (tehát a másik ikertől jövő jelek megváltozása) Béla számára 3 év után félidőben, Antal számára 9 év után, egy évvel az újra találkozás előtt történt. Természetesen a villogó órákat helyettesíteni lehet mondjuk adott hullámhosszúságon folytonosan sugárzó lézer fényforrásokkal, de a Doppler-eltolódás pontos meghatározásához ekkor a beérkező jelzőfény hullámhosszúságát pontosan meg kell tudni mérni.

Az igazi történet

A fenti történetben egy ikertestvérpár, Antal és Béla szerepelt, de valójában Ádám, és Éva volt a két főszereplő. Éva két évvel idősebb volt Ádámnál, ennek ellenére egymásba szerettek. De a környezetük nem nézte jó szemmel ezt a kapcsolatot, mondván Éva idősebb, és ellenkezik a helyi szokásokkal. Ezért Éva jelentkezett az űrutazásra, ami számára csak 6 évig tartott, míg Ádám 10 évig várta, hogy Éva visszatérjen. Ez meg is történt, és ekkor Éva két évvel volt fiatalabb Ádámnál, így a korkülönbség már nem jelentett akadályt. De hogy a kapcsolat hogyan élte túl a 10, akarom mondani 6 év távollétet, azt nem tudom megmondani, az olvasó találgatásra van utalva.

Utószó

A példában konkrét számértékeket használtam Doppler-eltolódásokra, időtartamokra, távolságokra, sebességekre, amit persze könnyű általánosítani, ha ezen számok helyett változókat használunk. Ezt a feladatot azonban az olvasóra hagyom gyakorlásnak, és arra is biztatom, hogy más, reálisabb számértékekkel is végezze el a számítást.

Azt az igen gyakori félreértést is el kell oszlatni, hogy az ikrek korkülönbsége a Béla által elszenvedett gyorsulásból adódik, hiszen, mint az látható, ezt az időszakot a példánkban nem is vettük figyelembe, kizárólag azokat az időszakokat tekintettük, amíg Béla súlytalanul lebegett, és Antal esetében is eltekintettünk a földi gravitációs gyorsulás, vagy a Föld forgásának jelenlététől. Természetesen Béla mozgásállapot-változásai nélkül nem állhatna elő ez a példa, de a korkülönbség az inerciarendszerekben eltöltött időtartamokból, az inerciarendszerek viszonyaiból, és váltogatásából következik. Ha ugyanezen sebesség váltogatások feleakkora úton és ennek megfelelően fele időtartammal következnének, úgy az ikrek korkülönbsége is feleakkora lenne, pedig a szükséges gyorsításoknak ugyanakkoráknak kellene lennie az ugyanakkora sebességkülönbségek eléréséhez. Ha az egész eseménysort végig egyetlen, de tetszőleges inerciarendszerből vizsgálnánk, akkor megállapíthatnánk, hogy Antal életvonala egyenes, ami a négydimenziós Minkowski térben éppen a leghosszabb időtartamot jelenti a lehetséges görbe, vagy tört vonalú életvonalakhoz képest, mint amilyen például Béla életvonala.

A gyorsulás a vele ekvivalensnek tekintett gravitációs vonzással csak Einstein általános relativitás elméletében játszik fontos szerepet. De itt már az inerciarendszerek (a forgómozgás abszolút jellegével együtt) is elvesztik globális használhatóságukat, és a természettörvények csupán a lokális pillanatnyi jelenlét (itt és most) számára lesznek egyenértékűek a téridő bármely pontjában, és meg kell elégednünk azzal a közelítéssel, hogy egy szabadon eső téridő pont kellően kicsiny környezete olyan, mintha Minkowski téridő lenne, mintha ez az egy pont egy inerciarendszer pontja lenne.

Az eddigiekből látható, hogy a téridőt egybetartó elektromágneses mező fénysebességű rezgésállapotainak, vagyis a fénysugarak útjának követésével, és két pontos órával nagyon sok fontos információ kinyerhető a modellünkből, anélkül, hogy a bonyolult koordináta, vagy sebesség transzformáció képleteire hivatkoznánk, vagy egymást keresztező órák végtelen sorozatait kellene szinkronizálnunk előzetesen, majd ezek méréseit utólagosan kellene továbbá összegyüjteni, ahogy az Einstein népszerűsítő könyvében, és az ezt tolmácsoló tankönyvekben olvasható. Ehhez szem előtt kell tartani azt a tényt is, hogy minden egyes fénysebességű rezgés, vagy más fénysebességű jel minden inerciarendszerben maradék nélkül megjelenik, csak legfeljebb más frekvenciával, más gyakorisággal. Ez persze nem jelenti azt, hogy megúszhatjuk a relativitás elmélet megértését, vagy az utószóban tett megjegyzéseim megértését ezen tankönyvek tanulmányozása nélkül, mindenesetre ezen példa megismerése nyomán talán már sokkal könnyebben megérthetjük az ott leírtakat.

A speciális relativitás elmélet hagyományos megismerését nagyban megnehezíti az azonos idejű koordináta rendszerek alkalmazása, illetve több ilyen koordináta rendszer közötti gyakori transzformáció kényszer, jó lehet ezeknek nincs valódi gyakorlati jelentőségük a relativitás elméletben, sőt, éppen ezen példákból látható, hogy miért is fölösleges erőltetni a newtoni rendszerben amúgy kiválóan használható abszolút rendszereket. Tudomásul kell venni, hogy az égen látható több millió fényévre levő csillagokhoz gyakorlatilag értelmetlen velünk azonos idejű koordináta rendszert kijelölni, hiszen csak egy több millió évvel ezelőtti állapotot látunk csupán az égen. Azóta az univerzum ezen távoli részein egészen más világ van, amelyről szerencsés esetben újabb évmilliók múlva fognak csak tudomást szerezni utódaink. Tehát a sok fölösleges, és bonyolult koordináta transzformáció a különféle inerciarendszerek között még félrevezető is. A távolságkontrakciót, vagy idődilatációt soha senki sem fogja látni, vagy érzékelni, mivel azok csupán az önkényesen és szinte kizárólag elvben kijelölt koordináta rendszerekben léteznek, és így elvben remek alkalmat adnak temérdek elvi számítás elvégzésére, ami igen hatásosan pallérozza az elmét, még ha kevés is a gyakorlati jelentősége. Egy fénysebességhez közeli objektum esetében már az objektum észlelése is gondot okoz, így az objektumok relativisztikus geometriai méretváltozása túl van a közvetlenül megfigyelhető jelenségek körén. Ezzel szemben egy óra járásának, vagy egy fénysugár frekvenciaváltozásának megfigyelése az elemi mérések közé tartozik, és a belőle levonható következtetések gyorsabban elvezetnek a relativitás elmélet megértéséhez. Az univerzum jobb megismeréséhez leggyorsabban a fénysugarak elemzése vezet.

Takács Ferenc bp. 2012. július 25.